今回は、プロスペクト理論の詳細について、表を用いて解説します。
プロスペクト理論の詳細
プロスペクト理論は、意思決定が規範から逸脱する理由の理論です。
つまり、カーネマン氏とトヴェルスキー氏の論じた意思決定モデルです。
具体的には、損失回避に関する理論です。
プロスペクト理論の詳細→投資における【 プロスペクト理論とは 】人の心理を投資に活かす
そしてここからがプロスペクト理論の応用です。
プロスペクト理論は、フォン・ノイマン氏とモルゲンシュテルン氏の期待効用理論に、①確率荷重②参照点3損失忌避の3つの特徴を新たに加えて定式化されます。
プロスペクト理論に従う意思決定者は、期待値や期待効用理論と似た計算で選択肢を評価します。
ただし、
・利得は主観的価値V(X)
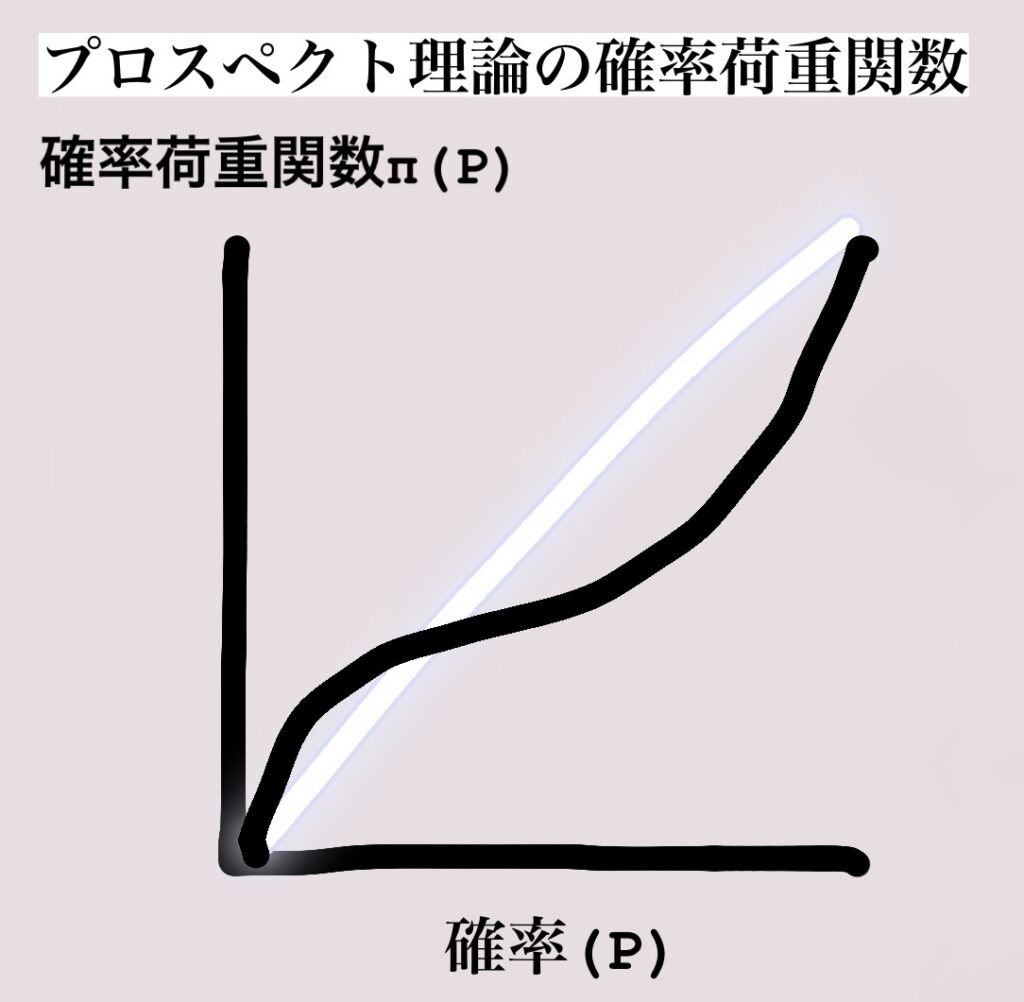
・確率は確率荷重(心理的評価)
・関数π(P)
によって評価します。
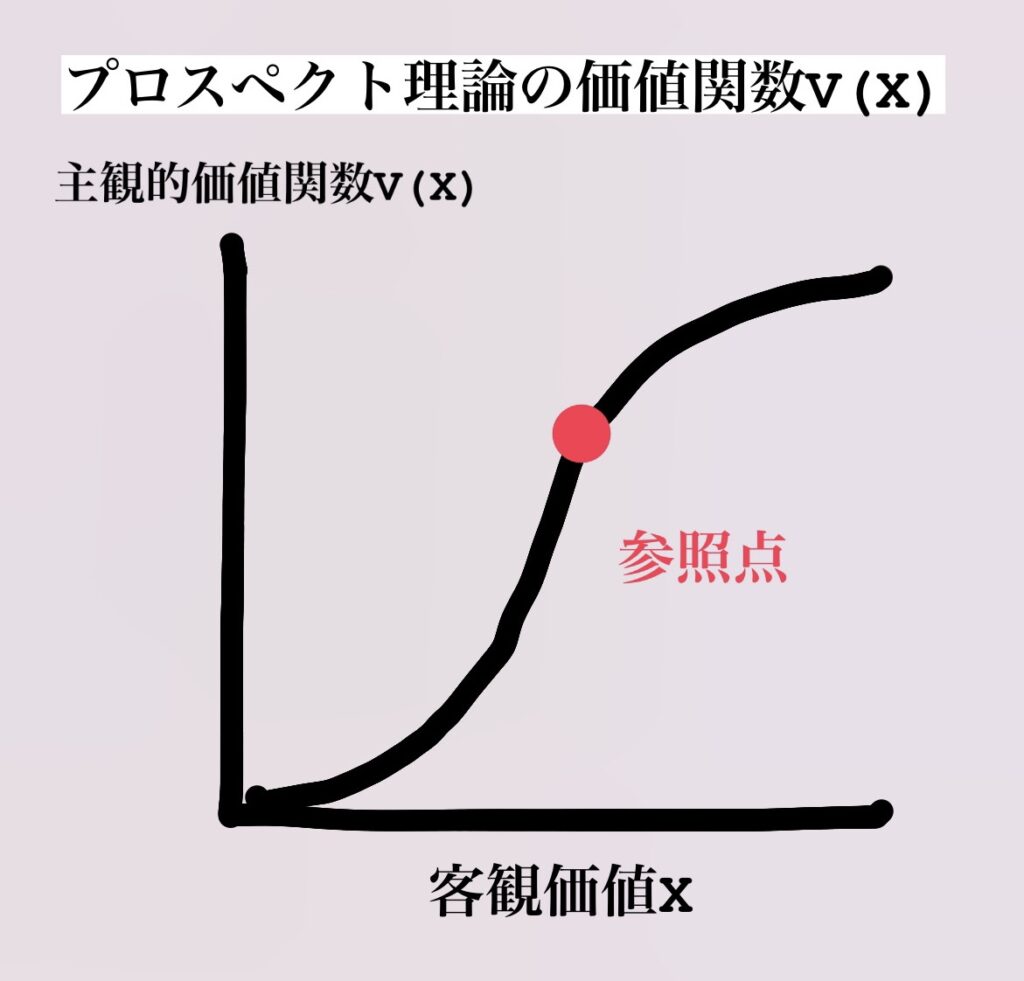
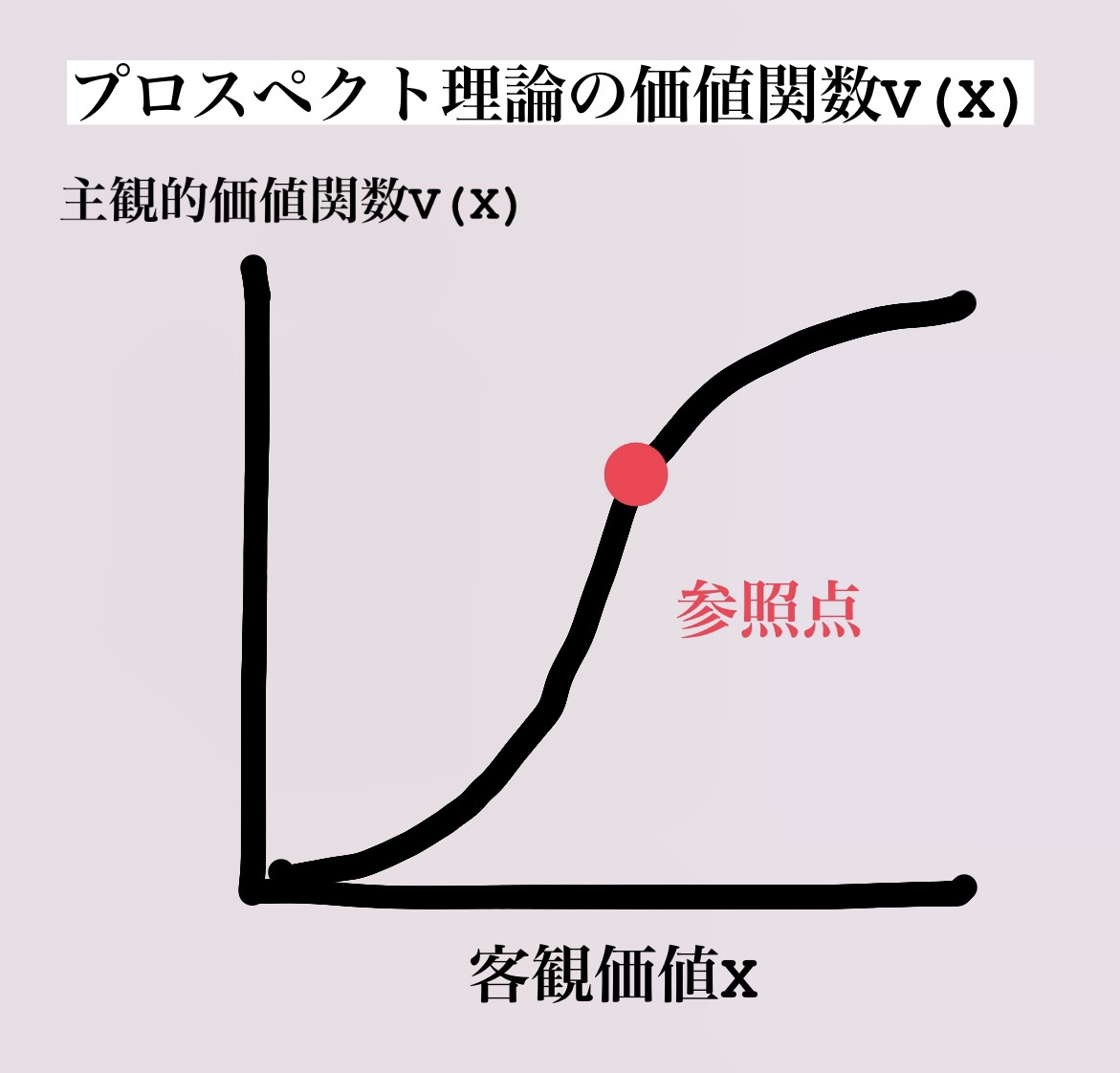
価値観数V(X)は、意思決定者の参照点と照らし合わせて、利益の領域で上に凸、損失の領域で下に凸の形となります。
上に凸の関数は、利益領域におけるリスク忌避傾向を表し、下に凸の関数は、損失領域におけるリスク志向傾向を表しています。
参照点は意思決定者にとって価値判断の基準であり、客観価値がゼロである時の「原点」とは必ずしも一致しません。
多くの場合、決定場面での現状が参照点であり、現状が変化すれば参照点も変わります。
また、V(X)は利益より損失の勾配が急です。
この損失の急勾配が損失忌避を表しています。
損失忌避は、ある金額を得る喜びよりも同じ金額を失う痛みの方が心理的な変化が大きいことを意味しています。
プロスペクト理論によるアレの逆説の説明
プロスペクト理論は、さまざまな非合理的決定現象を説明しうることにより高い評価を得ました。
上記のアレの逆説を検討しましょう。
プロスペクト理論では、CD間でのDの選好およびAB間でのAの選好を、各々次のように表します。
π(0.1)*V(250)>π(0.11)*V(100)
V(100)>π(0.1)*V(250)÷π(0.89)*V(100)
これらのことから、
100>π(0.11)+π(0.89)
が導かれます。
つまり確率Pに対するπ(P)の値は、一般にPより小さいです。
よってπ(P)は上記のしきを満足させます。
すなわち、アレの逆説はプロスペクト理論とは矛盾しないのです。
同様に、、「アジア病気問題」でも損失忌避が見られています。
まとめ
人間は、同じ額だったとしても、利益を得る時と損失を被る時だったら、損失を被る時の方が嫌がるということです。
その結果、損失回避の選択をする傾向があるということです。
今回はプロスペクト理論の詳細を説明しましたが、経済的心理学においてプロスペクト理論はよく用いられているし、実際の投資においてもこの心理がよく働いているため、必須で覚えておきましょう。




最近のコメント